How the Arbatel Spirits Got Their Names

Buckle up, bastards. It’s about to get heavy.

The Arbatel, first published in 1575, may be the most influential book on ritual magic ever written. Its straightforwardness has made it popular since its first appearance and it is a common choice as first grimoire for budding occultists.

The Arbatel presents (among other things) the “Olympic spirits,” seven powerful beings “by whom God hath appointed the whole frame and universe of this world to be governed” (Turner’s 1655 translation). There is one spirit for each of the Ptolemaic “planets”—the sun, the moon, and the five planets of the solar system known at that time.

Now, we know of no grimoire before the Arbatel that uses these spirit names. Nor do these spirit names come from any known mythological system. Nor do they all come from the same language. Hagith might be Hebrew—it is, in fact, the name of a minor character in the Hebrew Bible—and Bethor might plausibly be derived from the Hebrew, as well. But Ophiel and Aratron both seem Greek, and the possible linguistic derivation of Phul is anyone’s guess.

The names seem varied, weird, and arbitrary. So where did the author of the Arbatel get them? Revelation? The random scattering of letters? Speaking in tongues? The mouths of the spirits themselves? Where did these weird names come from?

The answer to this question is easy once we remember one important fact: the history of the occult is tightly interwoven with the history of cryptography. Where we find codes and ciphers written about in the early modern period, we will frequently find the occult written about, too.

Consider Johannes Trithemius (1462-1516). He is sometimes called the father of modern cryptography, in part because he published the first printed work on the subject; he also numbered among his students the occultists Heinrich Cornelius Agrippa and Paracelsus. There have been lengthy scholarly arguments about whether his most famous work, the Steganographia, is about magical spirits or about codes and ciphers.

For our purposes, Trithemius’s most important contribution is the cipher that bears his name. If you fiddled around with codes and ciphers as a kid like I did, you probably worked with simple substitution ciphers: A=1, B=2, and so on. You encode your message into numbers, and your recipient uses the cipher to get the message back. Or you may have seen the so-called Caesar cipher, in which each letter of a message is shifted down a certain amount—say, five letters. Thus, an A in the message would be replaced by an F, a B would be replaced by a G, and so on.

Such simple ciphers are easily broken because some letters are more common in English than others. If you see a particular character showing up a lot, it is probably a common letter like E, A, T, or S, for example. Trithemius had a bright idea for complicating things. What if instead of just a single cipher, the person writing the message used several? And this is where the tabula recta comes in. This is a table with 26 alphabets written on it in rows, with each alphabet shifted over one space relative to the one above it.

You could start at, say, the sixth row. You encode the first word of your message using this row of the tabula recta. But instead of encoding the whole message this way, you can shift down—say, four rows, ending up at row 10—to encode the second word of the message. Go down four more rows, to row 14, in order to encode the third word, and so on. Basically, instead of being a simple substitution cipher, the Trithemius is a polyalphabetic substitution cipher, making it very much harder to break.

And here is the point: whoever wrote the Arbatel used a tabula recta—a Trithemius cipher—to get the names of the spirits.

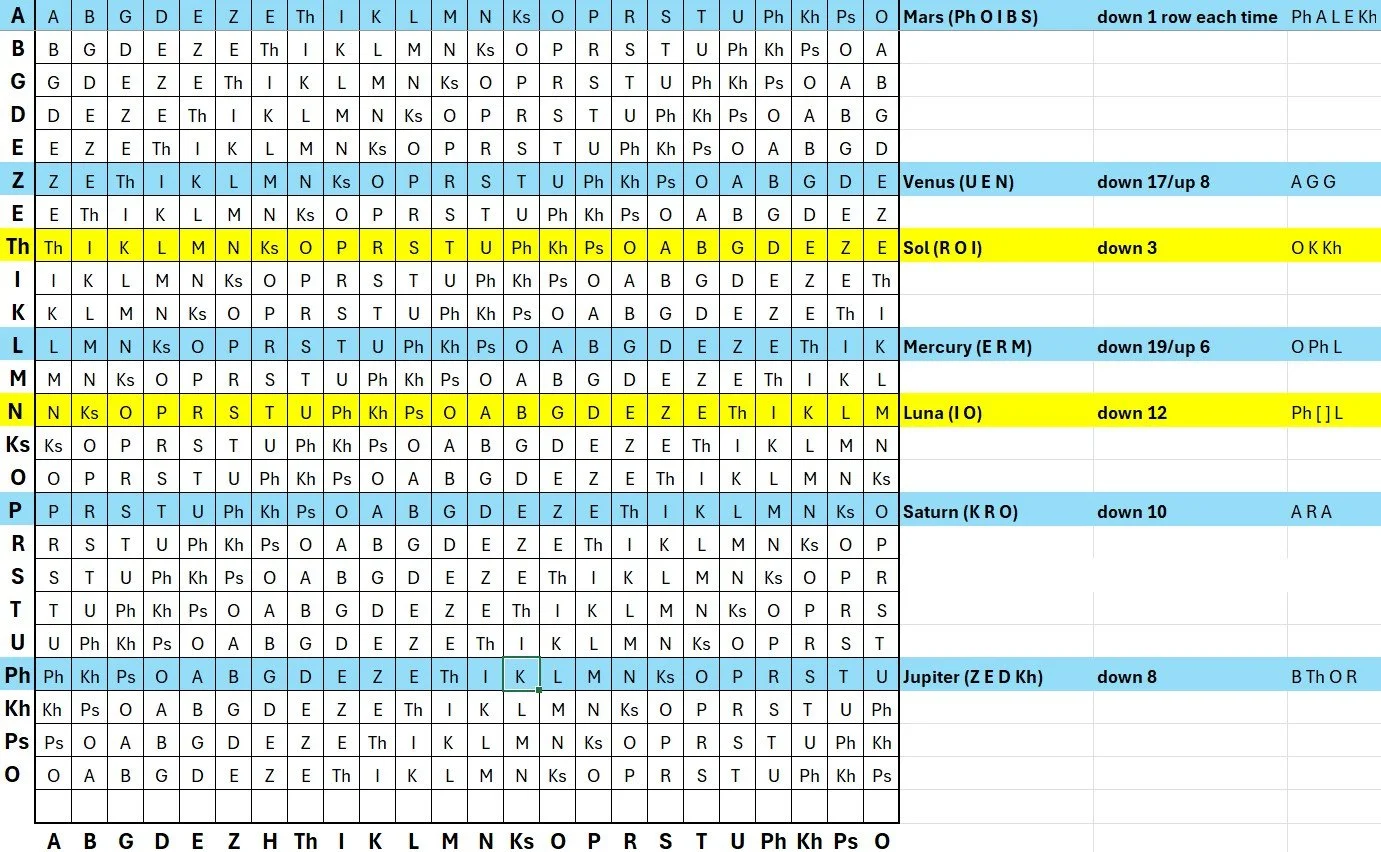
Now these are “Olympic spirits,” “spirits of Olympus,” spirits whose names come from “the Olympic speech.” Greek, right? Our tabula recta will use the Greek alphabet of 24 letters, and not our Roman alphabet of 26. Here it the tabular recta used by the author of the Arbatel, whom we will call François since scholars believe that he was a French Paracelsan.

(Since many people lack intimacy with the Greek alphabet, I have transliterated the letters into rough phonetic equivalents: alpha is A, beta is B, epsilon and eta are both E, omicron and omega are both O, and so on. The only peculiarity is that a blank line is added, so that the tabula has 25 rows instead of the 24 you’d expect from its use of the Greek alphabet.)

Tuesday, named after the Norse war-god Tyr, is associated with Mars (in Latin, Dies Martis). For whatever reason—there may be a clear justification or it may be arbitrary, I’m still investigating—François started with the first row, where alpha = alpha, beta = beta, and so on. François then went down by one alphabet for each letter. And what did François encode in order to get the spirit-name Phaleg? Sensible choices like Ares, Mars, and Tyr appear not to have worked, so he (he?) cheated a bit and used Ph O I B S—perhaps because of the common confusion of Apollo’s epithet Phoebus and the name of Ares’s son, the fear-god Phobos. Starting at row 1 and going down one row for each letter, the result is Ph A L E Kh (phi alpha lambda epsilon chi).

Wednesday is associated with Mercury (Dies Mercurii). The writer started at row 11 and went down 19 rows (or up 6 rows, same difference) for each letter. The text being encoded was E R M, the first three letters of Hermes’s Greek name (the H sound was done with a diacritical mark). The output? O Ph L.

Thursday, Jupiter, starts at row 21 and goes down 8 rows for each letter. Here the author cheats a bit by using (roughly) the Hebrew word for the planet Jupiter, Tzedek (Z E D Kh). The output is B Th O R.

Friday, Venus, really should start at row 31 to keep the pattern going. Unfortunately, there are only 25 rows in our tabula recta. So we wrap around, and Venus starts at row 6, and it goes down 17 rows (up 8 rows) for each letter. The input is Venus, or at least the first three letters of that name: U E N (upsilon is the most sensible choice for the V that the Greek alphabet lacks). The output is A G G.

Saturday, Saturn, begins, as we might expect, on row 16. It goes down 10 rows for each letter. The input is the first three letters of Kronos’s name, K R O, and the output is A R A.

Some things to notice: first, going in order of the Latin days of the week, the starting row is 10 down each time: Tuesday’s spirit starts at 1, Wednesday’s starts at 11, Thursday’s at 21, and so on, as we have already seen.

Second, François sometimes struggles to find a good spirit name. We see him using both Hebrew and Greek, and even stretching things a bit (Ph O I B S for Ares). It is as though François has stuck himself with a system for what row to start on and how far down to go for each letter, and this rigor makes good spirit names harder to derive from the tabula recta. (Again, I have not yet been able to figure out what decides how many rows the writer moves down with each new letter.)

Third, François frequently just uses the first three letters of plaintext to produce the start of a spirit name, then slaps on a suffix. Thus the tabula recta gives him A G G for the Venusian spirit, and he slaps on the Hebrew suffix -ith. A R A gives the Saturnian spirit, and he slaps on the Greek suffix -tron. He seems to feel that getting a workable trio of letters is close enough for government work.

But this just gives us the five planets. What about our solar system’s two luminaries, the sun and the moon, Sunday and Monday? Here, I confess that I am puzzled. It is clear to me how the names were derived, but not why.

Thus, our writer uses the French word for king (transliterated into Greek) to get the name of his solar spirit—R O I yields O K Kh—which suggests a lot of difficulty getting his cipher to give him a workable output. Why not use an input like Apollo, Helios, or Sol? Similarly, the writer uses Io’s name to get Ph [ ] L, where the middle letter falls on the blank row. Why not instead use Selene, Luna, or Levanah? François seems to be stuck starting from a particular alphabet and going down a particular number of rows each time, so that he has a hard time getting a spirit name that works.

But why should the name of the solar spirit start at row 8 and go down 3 each time? Why should the lunar spirit start at row 13 and go down 12 each time?

I have absolutely no idea.

But be that as it may, this is how the writer of the Arbatel derived the names of his spirits. A Trithemius cipher, a tabula recta, using the Greek alphabet.

Yeah, I did this in Microsoft Excel. You want to make something of it?

This answer opens up all kinds of new questions, however. What determines how many rows to go down each time? Why doesn’t anything seem to start on rows 3, 18 or 23? Might the author’s own name be encoded in this tabula recta? And might the title of the Arbatel be itself derived from this table, as well?

And then there is the question of how generalizable my finding is. Might the names of at least some spirits in other grimoires be similarly derived? When we see Goetic demons with names like Gaap, Aym, Ipos, and Bune, are we in fact seeing the outputs of another tabula recta? Or perhaps something fancier, like a Vigenère cipher?

I will be interested to see where further research in this area takes us. I would also be interested to see if anyone else has independently figured out the derivation of these spirit names—in retrospect, the answer seems so obvious.

And if you develop new insights about how the Arbatel author used this tabula recta, do let us all know!